Wallpaper groups and Art


When talking about the regularity of patterns in modern art, one often mentions Maurits Cornelis Escher. He was born in Leeuwarden on June 17, 1898, and died in Hilversum on March 27, 1972. After studying at the “School voor Bouwkunde, Versierende Kunsten en Kunstambachten” in Haarlem, he traveled several times to places like Spain, where he studied Moorish art at the Alhambra. Here, he found inspiration for his infinite tessellations.

Mosaic copy of an Alhambra tile

Escher used the wallpaper groups only as a study of patterns for his further works. Think, for example, of “Sky and Water II,” a woodcut from 1938. Or think of the lithograph “Reptiles” from 1943. In these works, the regularity of the group is used to make a transition from one to the other. In “Sky and Water II,” the woodcut transitions from birds to fish in a gradual transformation.

In the lithograph “Reptiles,” we have a transition from a flat surface to a spatial one, as the little lizards seem to crawl out of the sheet of paper.

Other Artists

There are more artists who use wallpaper groups in their artistic expressions. On the site https://tiled.art/en/artists/, you can find several artists along with their work. Here is an example of Francine Champagne:

Often you can see that the tessellations consist of one or more polygons. This is always the case, even if it is difficult to see. In a following blog, we will look at the following two subdivisions: Heesch type and Isohedral type.

Back to wallpaper groups. If you’re wondering which group a particular pattern belongs to, ask yourself the following question: How many times can you rotate the pattern at most? As we have seen before, this can be 1, 2, 3, 4, or 6 times. Call this number n.

  • For n = 1 there are no rotations, still we can ask ourselves if we can mirror the tile:
    • The design has a reflection and a glide reflection. We have found a group called cm.
    • There is a reflection but nog a glide reflection, this is group pm.
    • There is no reflection, but there is a glide reflection, now we’re dealing with group pg.
    • There isn’t any mirroring, we end up in group p1.
  • When n = 2, we can rotate over 180 degrees. Again we ask ourselves if we can apply mirroring, but now the mirror axes can go into two different directions:
    • We have reflections in two different directions. Now we ask ourselves whether the reflections run over the rotation points.
      • When rotation points are no the mirror axes, we consider pmm.
      • However when the rotation points are not on the mirror axes, we have group cmm.
    • When the mirror axes are parallel (so not crossing), we have group pmg.
    • When there is no reflection but there is a glide reflection, we have group pgg.
    • Without any reflection and glide reflection we have p2.
  • If we can rotate by 120 degrees, so if n = 3:
    • If there is also reflection, then we again look at the rotation points.
      • All rotation points on the mirror axes give us the group p3m1.
      • But if one is not on the rotation points, then we have the group p31m.
    • If there are no reflections, then we have the group p3.
  • For a 90-degree rotation (n = 4):
    • For reflections, we check whether they are parallel or intersect at 90 degrees.
      • Mirror axes at 90 degrees to each other indicate the group p4m.
      • Otherwise (if the mirror axes are parallel), then we have the group p4g.
    • Without reflections we have the group p4.
  • n = 6, so rotation by 60 degrees:
    • For a reflection, the group is p6m.
    • If there is no reflection, we consider the group p6.

Get started yourself!

You might find the idea of creating your own pattern appealing. Think about the smallest space in which you’d like your repeating “figure” to fit. This space should be completely filled and should not overlap when the pattern is repeated on your paper. Practically speaking, this means you have a choice among five different “areas”.

This start determines the grid you will work with. It also determines which symmetries you can and want to use in your further work. The 5 grids you can choose from are:

  • Oblique lattice: The lines of your grid (the straight lines where your grid points lie) have an angle other than 90 degrees. They are also at two different distances from each other. This creates many limitations in your further choices; you can choose a rotation of 180 degrees or no rotation. (Wallpaper pattern groups p2 or p1)
  • Rectangular lattice : The lines of your grid are at 90 degrees to each other, but they are at two different distances from each other. In this grid, we can rotate 180 degrees, as well as reflect and glide-reflect, and also both at the same time (so, we can now choose from the wallpaper pattern groups pm, pg, pmm or pmg)
  • Rhombic lattice: This grid is formed by taking the rectangular lattice and, alternately, skipping a grid point. As it were, you do not look at the neighboring points. (This grid is a kind of inverse of the rectangular lattice; more on this in a future post). Apart from rotation, we can also do the same like we did with the rectangular lattice (cm of cmm or pgg).
  • Square lattice: The lines of your grid are at 90 degrees to each other, and all lines are equidistant from each other. In this grid, we rotate 90 degrees and also have the choice to reflect or glide-reflect. (This grid is as it were an inverse of itself; more on this in a later blog) (p4, p4m or p4g)
  • Hexagonal lattice: The points of your grid are equidistant from each other and can initially be rotated 60 or 120 degrees. There is also the choice to reflect and/or to let the reflection lines run over the rotation points or not. Glide-reflection is not an option here. (We can choose from the following wallpaper pattern groups: p6, p6m, p3, p3m1 or p31m)

To make your wallpaper more attractive, you can ensure that your pattern doesn’t align straight with each other. However, it is easy to start with polygons that match your chosen grid and apply transformations (rotation, mirroring or potentially glide reflection).

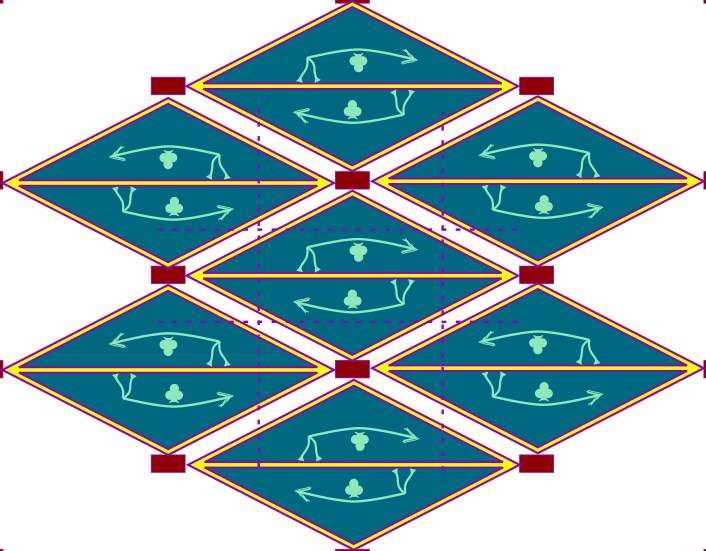
Now you want to make your pattern more interesting, and you can do this by, for example, adjusting the straight sides of the diamond. Of course, this must be done in such a way that the properties of your pattern remain intact. In this case, it means that if you create a protrusion at the top left of your triangle, it will mean a notch of the same shape at the bottom right of that triangle.

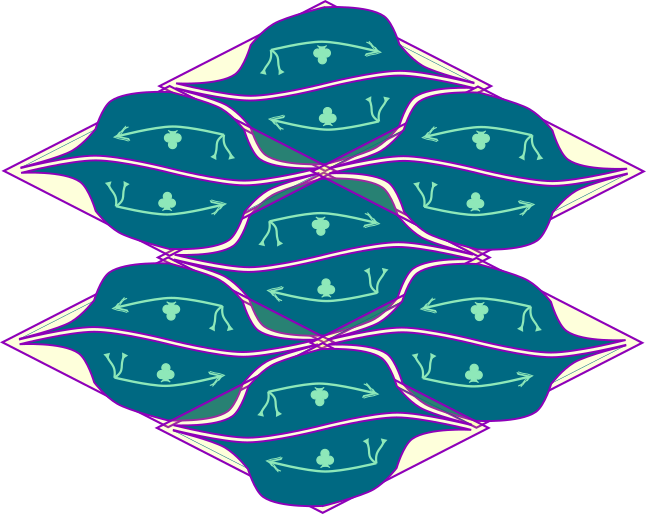
And so you can continue until you are satisfied. Of course, it is fun to add some color and make the shapes explicit. Despite imposing limitations on yourself, you can still be very creative: Limitations make you creative.

In the above design, you could see five strips. Analogous to the wallpaper groups, you can do the same with wallpaper strips. Instead of being able to slide two sides, you can now only slide one side. I will return to this in a later blog.

References

Related Posts